1. Définitions
Il s'agit d'arbres binaires étiquetés aux sommets. L'étiquette d'un sommet x est la clé ou le contenu du sommet.
Contrairement à un arbre binaire général, les clés d’un ABR doivent être comparables entre elles.
Ainsi, un ABR a les propriétés suivantes :
- les clés du sous-arbre gauche d'un nœud sont inférieures (ou égales) à la clé du nœud.
- les clés du sous-arbre droit d'un nœud sont strictement supérieures (ou égales) à la clé du nœud.
2. Quelques primitives de la SDA arbre binaire de recherche
2.1. Chercher le maximum dans un ABR
L'algorithme de recherche de la plus grande clé dans l'ABR
Fonction maximum_recur(ABR)
"""
Entrée : ABR est un arbre binaire de recherche ;
Sortie : la plus grande clé dans ABR.
"""
Si ABR est vide :
renvoyer None
Si ABR.droit est vide :
renvoyer ABR.cle
Sinon :
renvoyer maximum_recur(ABR.droit)
FinFonction
Faites-vous plaisir 1 :
Écrire l'algorithme de recherche de la plus petite clé dans l'ABR, minimum_recur(ABR).
2.2. Test d'appartenance
Pour savoir si une clé x est présente, on compare x à la clé du nœud courant :
- si
xest plus petite, on descend dans le sous-arbre gauche ; - si
xest plus grande, on descend dans le sous-arbre droit ; - si
xest égale, on a trouvé la clé.
Le pseudo-code de la fonction rechercher_recur
Fonction rechercher_recur(ABR, x)
"""
Entrée : ABR est un arbre binaire de recherche ; x est une clé.
Sortie : True si x appartient à ABR, False sinon.
"""
Si ABR est vide :
renvoyer False
Si x = ABR.cle :
renvoyer True
Si x < ABR.cle :
renvoyer rechercher_recur(ABR.gauche, x)
Sinon :
renvoyer rechercher_recur(ABR.droit, x)
FinFonction
2.3. Insérer une donnée dans ABR
Pour insérer une valeur x, on descend dans l’arbre comme pour une recherche,
jusqu’à trouver un emplacement vide.
Le pseudo-code de la fonction d'insertion
Fonction inserer_recur(ABR, x)
"""
Entrée : ABR est un arbre binaire de recherche ; x est une clé.
Sortie : x est insérée dans ABR (modification en place).
"""
Si ABR est vide :
ABR ← nouveau_noeud(x)
arrêter
Si x < ABR.clé :
Si ABR.gauche est vide :
ABR.gauche ← nouveau_noeud(x)
Sinon :
inserer_recur(ABR.gauche, x)
Sinon :
Si ABR.droit est vide :
ABR.droit ← nouveau_noeud(x)
Sinon :
inserer_recur(ABR.droit, x)
FinFonction
3. Implantation chaînée
3.1. Créer un arbre binaire de recherche
In [1]:
class Noeud:
"""Modélise un noeud d'un arbre binaire."""
def __init__(self, cle, gauche = None, droit = None):
self.cle = cle
self.gauche = gauche
self.droite = droit
#Afficher le noeud
def __str__(self):
"""Affiche la valeur (cle) du noeud."""
return f"{self.cle}"
def __repr__(self):
"""Affiche le noeud."""
return f"Noeud({repr(self.cle)},
{repr(self.gauche)},
{repr(self.droit)}
)"
class ABR:
"""Représente un arbre binaire."""
def __init__(self, racine):
self.racine = racine
#Afficher l'ABR
def __repr__(self):
"""Affiche l'objet arbre binaire."""
return f"ABR({repr(self.racine)})"
def est_vide(self):
"""Renvoie True si l'ABR est vide, False sinon."""
return self.racine is None
def get_gauche(self):
"""
Renvoie le sous-arbre gauche.
Si l’arbre est vide, on renvoie ABR(None)
"""
# à compléter
def get_droit(self):
"""
Renvoie le sous-arbre droit.
Si l’arbre est vide, on renvoie ABR(None)
"""
# à compléter
def afficher_infixe(self):
"""Affiche l'ABR (gauche, racine, droit)."""
if self.racine is None:
return None
self.get_gauche().afficher_infixe()
print(self.racine.cle, end=" ")
self.get_droit().afficher_infixe()
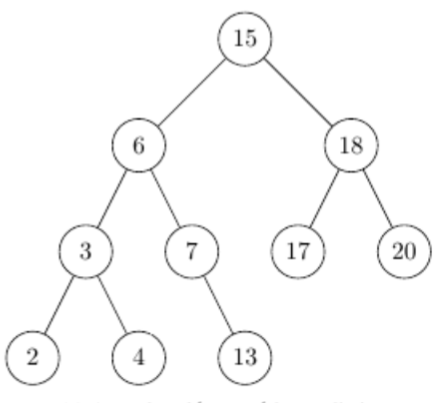
Un exemple :
In [2]:
# implémentation de l'ABR gauche
noeud2 = Noeud(2)
noeud3 = Noeud(3)
noeud4 = Noeud(4)
noeud6 = Noeud(6)
noeud7 = Noeud(7)
noeud13 = Noeud(13)
noeud15 = Noeud(15)
noeud17 = Noeud(17)
noeud8 = Noeud(18)
noeud20 = Noeud(20)
noeud3.gauche = noeud2
noeud3.droite = noeud4
noeud7.droite = noeud13
noeud6.gauche = noeud3
noeud6.droite = noeud7
noeud18.gauche = noeud17
noeud18.droite = noeud20
noeud15.gauche = noeud6
noeud15.droite = noeud18
mon_abr = ABR(noeud15)
Faites-vous plaisir 2 :
- Compléter les méthodes get_gauche et get_droit de la classe ABR.
- Donner, à la main, le parcours infixé de mon_abr ;
Que remarquez-vous sur l’ordre obtenu ? -
Traduire, en Python, la méthode d'ABR rechercher_recur dont le pseudo-code est donné ci-avant.
La tester avec- mon_abr et la clé 2025,
- puis mon_abr et la clé 13.
-
Traduire, en Python, la méthode d'ABR maximum_recur dont le pseudo-code est donné ci-avant.
Déterminer la plus grande valeur de mon_abr -
Écrire dans la classe ABR, la méthode taille qui renvoie la taille d'une instance de l'ABR.
L'appliquer à mon_abr. - Traduire, en Python, la méthode inserer_recur qui ajoute une clé donnee à l'ABR.
- Donner, à la main, les parcours préfixé et postfixé de mon_abr
Faites-vous plaisir 3 :
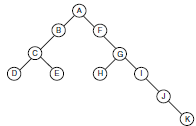
-
On donne l'arbre binaire ci-contre.
- Donner l'affichage préfixé, postfixé et infixé de cet arbre binaire.
- Donner l'affichage en largeur d'abord de cet arbre.
- Dessiner un AB dont l'affichage infixé est le suivant : CBIDFGE.
-
Un AB a huit nœuds. Les parcours postfixé et infixé de l'arbre sont donnés ci-dessous.
Parcours postfixé : FECHGDBA
Parcours dans l'ordre : FCEABHDG
Dessinez cet arbre. -
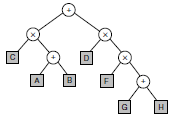
Donner les parcours préfixé, postfixé et infixé de l'arbre d'expression ci-dessous.
Faites-vous plaisir 4 :
- Dessinez tous les ABR possibles pour les données 5, 9 et 12.
-
-
Créez un ABR en utilisant les données suivantes entrées sous forme d'ensemble séquentiel :
14 23 7 10 33 56 80 66 70. - Insérer dans cet arbre 44 et 50.
-
Créez un ABR en utilisant les données suivantes entrées sous forme d'ensemble séquentiel :
-
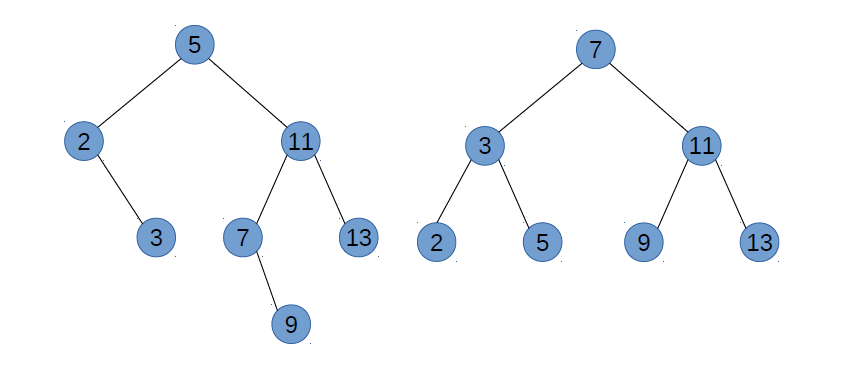
Lequel de ces deux arbres binaires est un ABR ? Justifier
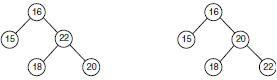
-
-
Créez un ABR en utilisant les données suivantes entrées sous forme d'ensemble séquentiel :
80 70 66 56 33 23 14 10 7. - Insérer 40 et 50 dans cet arbre.
-
Créez un ABR en utilisant les données suivantes entrées sous forme d'ensemble séquentiel :
- Visiter, à l'aide du parcours infixé, les nœuds de l'ABR ci-après.
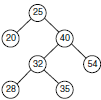
In [ ]: