récursivité

1. Pincipe

La récursivité est une manière d'implémenter un algorithme où une fonction s'appelle elle-même.
Une fonction récursive comporte deux éléments clés :

1. Cas de base (ou condition d'arrêt) : La situation où la fonction arrête de s'appeler elle-même.
2. Appel récursif : La fonction se rappelle avec des arguments modifiés pour se rapprocher du cas de base.

2. Structure d'une fonction récursive

def fonction_recursive(param):
    if condition_de_base:
        return résultat
    else:
        return fonction_recursive(param_modifié)

3. Exemples

Exemple 1 :
Écrire une fonction qui permet de calculer (sans utiliser len) le nombre d'éléments d'une liste.

# version itérative
def longueur_iterative(lst: list) -> int:
    """
        Calcule de manière itérative la longueur d'une liste sans utiliser len().
    """
    cpteur = 0
    for elt in lst:
        cpteur += 1
    return cpteur

# version récursive
def longueur_recursive(lst):
    """
        Calcule récursivement la longueur d'une liste sans utiliser len().
    """
    if lst == []: # cas de base
        # print("Liste vide : renvoie 0")
        return 0
    else: # cas récursif
        #print(f"Appel avec : {lst}")
        return 1 + longueur_recursive(lst[1:])

Exemple 2 : La factorielle d'un entier naturel
La factorielle d'un nombre est définie telle que :
n! = n×(n - 1)×(n - 2)×...×2×1
Avec
0! = 1 (cas de base)
n! = n(n - 1)! (cas récursif).

def factorielle(n):
    """Calcule la factorielle d'un entier naturel."""
    if n == 0:  # Cas de base
        return 1
    else:       # Appel récursif
        return n * factorielle(n - 1)

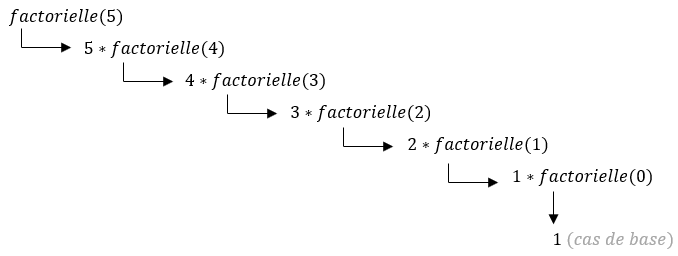
factorielle(5)

Arbre d'appel de factorielle(5)

Exemple 3 :
On considère la suite u_n définie sur l'ensemble des entiers naturels par :

• u₀ = 5
• u_n+1 = 2u_n + 3 pour tout entier naturel.

Écrire une fonction qui permet de calculer le terme d'indice n de cette suite.

# version récursive
def u_recur(n):
    if n == 0: # Cas de base
        return 5
    else:
        return 2*u_recur(n - 1) + 3 # Cas récursif

u_recur(4)

Arbre d'appel de u(4)

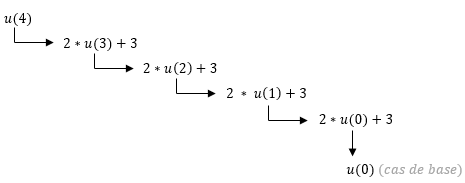
# Version itérative
def u(n):
    u = 5
    for i in range(1, n + 1):
        u = 2 * u + 3
        print(f"u({i}) = {u}")
    return u

import time
date_debut = time.perf_counter()
u(5)
date_fin = time.perf_counter()
dt_iter = date_fin - date_debut
print(f"La version itérative se fait en {dt_iter} secondes")

import time
date_debut = time.perf_counter()
u_recur(5)
date_fin = time.perf_counter()
dt_recur = date_fin - date_debut
print(f"La version récursive se fait en {dt_recur} secondes")

print(dt_iter/dt_recur)

4. Avantages et inconvénients de la récursivité

4.1. Avantages

• Clarté et concision
  Le code récursif est souvent plus lisible pour les problèmes naturellement récursifs.
• Adapté aux problèmes diviser-pour-régner
  Idéal pour résoudre des problèmes complexes en les décomposant.
• La récursion est souvent utilisée pour manipuler des listes chaînées, files et piles

4.2. Inconvénients

• Consommation mémoire élevée
  Chaque appel récursif occupe de la mémoire dans la pile d'exécution. Il y a par conséquent un risque de débordement de pile (stack overflow) : Si la condition d'arrêt n'est pas bien définie ou si le problème est trop grand, cela peut provoquer une erreur de débordement.
• Moins efficace
  La récursivité peut être inefficace pour certains problèmes si elle n’est pas combinée avec des optimisations comme la mémorisation (memoization).

5. D'autres exemples classiques

5.1. Suite de Fibonacci

• \(u_{0}=1\)
• \(u_{1}=1\)
• \(u_{n}=u_{n-1}+u_{n-2}\),\( \) \(\forall n\geq2\).

Écrire une fonction fib(n), définie de façon récursive, qui renvoie le terme de rang n de la suite \((u_{n})\).

def fibo(n):
    if n < 2:
        return 1
    return fibo(n - 1) + fibo(n - 2)

def fibo_iter(n):
    if n < 2:
        return 1
    else:
        a = 1
        b = 1       
        for i in range(2, n + 1):
            tmp = a + b
            a = b
            b = tmp
        return b

5.2. Somme des n premiers entiers non nuls

1. En utilisant la récursivité, écrire la fonction somme_recur(n) sachant que :
   
   • Si n = 0, somme_recur(n) = 0
   • Si n > 0, somme_recur(n) = n + somme_recur(n - 1)
2. Dessiner l’arbre d’appels de cette fonction pour l’appel somme_recur(5).
3. Parcourir cet arbre d’appels « à rebours » pour illustrer le fonctionnement de la fonction somme comme cela a été fait dans la version récursive de l'exemple 2.

5.3. Opération de puissance n-ième d’un nombre x

\(x^n=x\times x\times ... \times x=x\times x^{n-1}\)
Par convention \(x^0=1\)
On définit récursivement la fonction puissance(x, n) telle que :

• Si \(n=0\), \(x^n=1\)
• Si \(n>0\), \(x^n=x\times x^{n-1}\)

Cas de base : pour \(n=0\)

1. Écrire la fonction récursive puissance(x,n) qui calcule le nombre \(x^n\) pour tout entier naturel n.
2. Dessiner l’arbre d’appels de cette fonction lorsque x = 3 et n = 5.
3. Parcourir cet arbre d’appels « à rebours » pour illustrer le fonctionnement de la fonction puissance comme cela a été fait dans la version récursive du premier exemple du paragraphe I.

5.4. Inversion d'une chaîne

On définit récursivement la fonction inverser_recur(texte) sachant que :

• Si texte est vide, inverser_recur(texte) = ""
• Si texte n’est pas vide, inverser_recur(texte) = inverser_recur(texte[1:]) + texte[0]

1. Écrire la fonction récursive inverser_recur(texte) qui renvoie la chaîne texte inversée.
2. Dessiner l’arbre d’appels de cette fonction pour l’appel inverser_recur("NSI").
3. Parcourir cet arbre d’appels « à rebours » pour illustrer le fonctionnement de la fonction d’inversion, comme cela a été fait dans la version récursive de l’exemple 2.

Faites-vous plaisir :

1. Écrire une fonction récursive, somme_recur(n) qui permet de calculer la somme des éléments d'une liste.
2. Écrire une fonction récursive qui recherche un élément dans une liste.
3. Écrire une fonction récursive est_palindrome_recur qui teste si un mot est un palindrome.
   On appelle palindrome un mot qui se lit dans les deux sens comme « été » ou « radar ».
   
   • Cas de base :
     • si le mot est la chaîne vide, c’est un palindrome ;
     • si le mot ne contient qu’une seule lettre, c’est un palindrome.
   • Dans les autres cas : le mot est un palindrome si et seulement si la première et la dernière lettre sont égales et le mot tronqué de ses premières et dernière lettres est un palindrome