Bangoua-IT — Première — Circuits logiques (transistor et opérateurs booléens)

Objectif. Comprendre comment, à partir de transistors, on construit des portes logiques (NON, ET, OU, XOR) et savoir dresser les tables de vérité de circuits simples (additionneurs).

1. Du transistor aux valeurs booléennes

Un transistor est un composant électronique qui se comporte (dans un modèle simple) comme un interrupteur commandé. Suivant la tension appliquée sur une de ses bornes, il peut être :

bloqué : il ne laisse pas passer le courant (comme un interrupteur ouvert) ;
saturé : il laisse passer le courant (comme un interrupteur fermé).

On associe alors à ces deux états les valeurs booléennes :

état bloqué → valeur logique \(0\) (FAUX) ;
état saturé → valeur logique \(1\) (VRAI).

En combinant de très nombreux transistors, on construit des portes logiques, puis des circuits de plus en plus complexes (additionneurs, registres, processeurs…).

2. Variables et opérateurs booléens

2.1 Variables booléennes

Une variable booléenne est une variable dont la valeur ne peut être que \(0\) ou \(1\).
En logique :

\(0\) est aussi noté FAUX (False) ;
\(1\) est aussi noté VRAI (True).

En électronique numérique, ces valeurs sont représentées par des plages de tension :

une tension basse (proche de 0 V) représente le niveau logique \(0\) ;
une tension haute (proche de la tension d’alimentation) représente le niveau logique \(1\).

2.2 Notion d’opérateur booléen

Un opérateur booléen prend en entrée une ou plusieurs valeurs booléennes, et produit une valeur booléenne en sortie. Dans un circuit, il est réalisé par une porte logique.

Pour décrire complètement un opérateur booléen, on utilise sa table de vérité, qui indique la valeur de la sortie pour toutes les combinaisons possibles des entrées.

3. L’opérateur NON (NOT)

L’opérateur NON correspond à la négation logique. Il inverse la valeur : si une proposition est vraie, sa négation est fausse, et réciproquement.

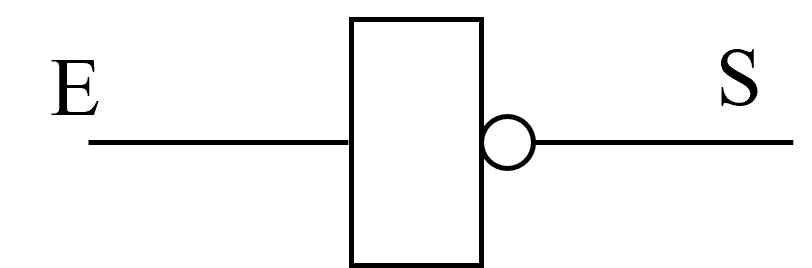
Symbole international de la porte NOT — Symbole international d'une porte NOT

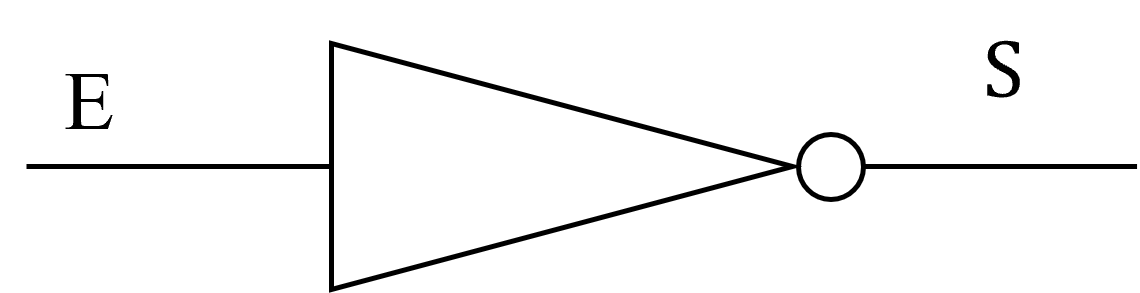
Symbole étasunien de la porte NOT — Symbole étasunien d'une porte NOT

Notations possibles :

\(non\ a = not\ a = \overline{a} = ¬a\)

\(a\)	\(\lnot a\)
\(0\)	\(1\)
\(1\)	\(0\)

Faites-vous plaisir 1 :
Compléter la table de vérité de l’expression \(\overline{a}\) pour \(a = 0\) puis \(a = 1\) (vérifier que vous obtenez bien la table ci-dessus).

4. Les opérateurs ET (AND) et OU (OR)

4.1 L’opérateur ET (AND)

La conjonction \(a\ et\ b\) est vraie uniquement si les deux propositions sont vraies. Dans tous les autres cas, elle est fausse.

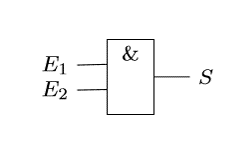
Symbole international de la porte AND — Symbole international d'une porte AND

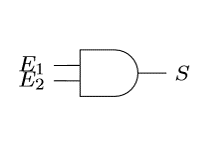
Notations possibles :
\(a\ et\ b = a\ and\ b = a ∧ b = a.b\)

\(a\)	\(b\)	\(a \cdot b\)
\(0\)	\(0\)	\(0\)
\(0\)	\(1\)	\(0\)
\(1\)	\(0\)	\(0\)
\(1\)	\(1\)	\(1\)

4.2 L’opérateur OU (OR)

La disjonction \(a\ ou\ b\) est vraie dès qu’au moins une des deux propositions est vraie. Elle n’est fausse que lorsque les deux propositions sont fausses.

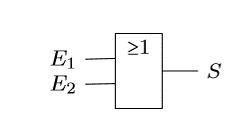
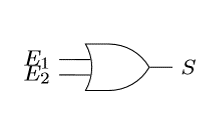
Notations possibles :
\(a\ ou\ b = a\ or\ b = a ∨ b\)

\(a\)	\(b\)	\(a \lor b\)
\(0\)	\(0\)	\(0\)
\(0\)	\(1\)	\(1\)
\(1\)	\(0\)	\(1\)
\(1\)	\(1\)	\(1\)

Faites-vous plaisir 2 :
Donner la table de vérité de l’expression logique \(\overline{a}.b\) (utiliser les tables de NOT et de AND).

5. Combinaisons de portes : l’opérateur XOR

On peut combiner les opérateurs de base pour construire de nouveaux opérateurs. Un exemple classique est le XOR (eXclusive OR).

Une expression possible pour XOR est :

\[ f(a,b) = \overline{a}.b + a.\overline{b} \]

Notation : \(f(a,b) = a ⊕ b\).

Faites-vous plaisir 3 :
Dresser la table de vérité de \(f(a,b) = \overline{a}.b + a.\overline{b}\).
Dans quels cas \(a ⊕ b\) vaut-il \(1\) ? Rédiger une phrase en français pour le décrire.

Interprétation : \(a ⊕ b\) vaut \(1\) si exactement une des deux entrées vaut \(1\).

6. Exemples de circuits : additionneurs

6.1 Additionneur 1 bit (additionneur « faible »)

Un additionneur faible (ou demi-additionneur) additionne deux bits \(E_{1}\) et \(E_{2}\) et produit :

un bit de somme \(S\) ;
un bit de retenue \(r\).

On peut le réaliser avec les opérateurs ET et XOR.

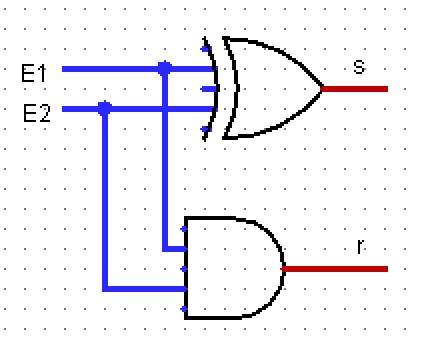
Schéma d’un additionneur 1 bit — Additionneur faible (1 bit).

Faites-vous plaisir 4 :
Dresser la table de vérité de l’additionneur faible : quelles sont les valeurs de \(S\) et \(r\) pour toutes les combinaisons possibles de \(E_{1}\) et \(E_{2}\) ?

6.2 Additionneur complet (additionneur « fort »)

Un additionneur complet (ou additionneur fort) additionne :

deux bits \(E_{1}\) et \(E_{2}\),
et une retenue d’entrée \(C_{in}\).

Il produit :

un bit de somme \(S\),
et une retenue de sortie \(C_{out}\).

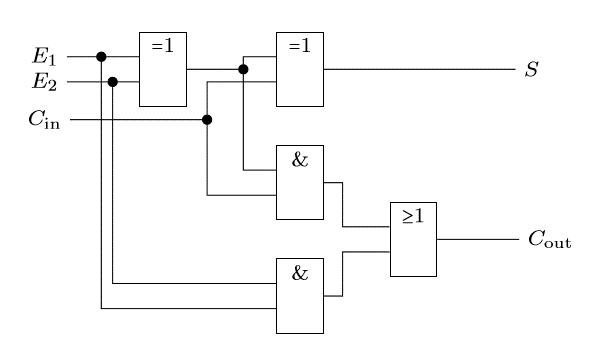
Schéma d’un additionneur complet — Additionneur fort (1 bit avec retenue d’entrée).

Faites-vous plaisir 5 :
Dresser la table de vérité de l’additionneur fort : pour toutes les combinaisons de \(E_{1}\), \(E_{2}\), et \(C_{in}\), donner S et \(C_{out}\).

7. Parenthèse Python : valeurs « vraies » et « fausses »

En Python, dans un contexte booléen (par exemple dans un if), certains objets sont considérés comme faux même si ce ne sont pas littéralement la valeur False.

Considérés comme Faux :

None et False ;
l’entier 0 et le flottant 0.0 ;
une chaîne de caractères vide "" ;
une liste vide [], un dictionnaire vide {}, un ensemble vide set(), etc.

Tous les autres objets sont considérés comme vrais dans un test conditionnel.