1. Définitions fondamentales
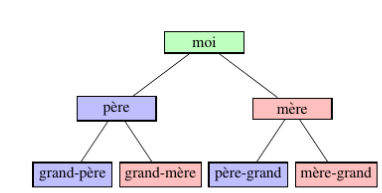
Un arbre est une structure constituée de nœuds reliés entre eux, organisée autour d’un nœud principal appelé racine.
Un arbre enraciné respecte les propriétés suivantes :
- chaque nœud, sauf la racine, possède exactement un parent ;
- un nœud peut avoir 0, 1, 2 ou plusieurs enfants ;
- on peut toujours atteindre un nœud depuis la racine en suivant un chemin unique ;
- il n’existe aucun cycle : on ne revient jamais à un nœud déjà visité en descendant.
Les éléments importants d'un arbre sont :
- Un nœud : représente une donnée ou un élément de l’arbre.
- Une arête : liaison entre un nœud et chacun de ses enfants.
- La racine : unique nœud sans parent, point de départ de l’arbre.
- Un parent : nœud situé directement au-dessus d’un autre.
- Un enfant : nœud situé directement en dessous d’un parent.
- Des frères : nœuds ayant le même parent.
- Une feuille : nœud sans enfant.
2. Représentation d’un arbre
a. Schéma conceptuel
A
┌───┼───┐
B C D
┌─┴─┐ ┌───┼───┐
E F G H I
Dans ce schéma :
- A est la racine ;
- B, C et D sont les enfants de A ;
- E et F sont les enfants de B ;
- C est une feuille (pas d’enfant) ;
- E, F, G, H et I sont des feuilles.
b. Représentation d’un arbre en Python
En Python, un arbre est représenté par son nœud racine.
Un nœud contient une valeur et une liste de nœuds enfants.
La racine est simplement le point d’entrée vers toute la structure.
class Noeud:
def __init__(self, valeur):
self.valeur = valeur
self.enfants = [] # liste de nœuds enfants
Exemple : construction de l'arbre suivant :
# A
# / | \
# B C D
# / \ / | \
# E F G H I
racine = Noeud("A") # ceci représente l'arbre entier
b = Noeud("B")
c = Noeud("C") # aucun enfant
d = Noeud("D")
e = Noeud("E")
f = Noeud("F")
g = Noeud("G")
h = Noeud("H")
i = Noeud("I")
racine.enfants = [b, c, d]
b.enfants = [e, f]
d.enfants = [g, h, i]
À retenir : on définit la structure d’un nœud, puis l’arbre complet est représenté par la variable contenant la racine.
3. Types d’arbres
3.1. Arbre général (ou n-aire)
Dans un arbre général, chaque nœud peut avoir autant d’enfants que nécessaire.
3.2. Arbre ordonné et non ordonné
- Arbre ordonné : l’ordre des enfants a une importance (on ne peut pas les permuter sans changer la structure).
- Arbre non ordonné : l’ordre des enfants n’a pas de signification particulière.
3.3. Arbre enraciné
Un arbre enraciné est un arbre dans lequel on a choisi une racine unique. Dans ce cours, nous travaillons toujours avec des arbres enracinés.
3.4. Arbres particuliers
Arbre symétrique
Un arbre est symétrique s’il est identique vu dans un miroir vertical (les sous-arbres gauche et droit se correspondent).
Arbre complet
Un arbre est dit complet lorsque tous les niveaux sont entièrement remplis (sauf éventuellement le dernier, qui peut être partiellement rempli).
Arbre équilibré
Un arbre est équilibré lorsque les hauteurs de ses sous-arbres restent proches. Cela évite des chaînes trop longues et permet des recherches plus efficaces.
Arbre dégénéré
Un arbre dégénéré est un cas extrême : chaque nœud n’a qu’un seul enfant. La structure ressemble alors à une liste chaînée verticale.
4. Propriétés importantes
4.1. Niveau
Le niveau d’un nœud est le nombre d’arêtes entre ce nœud et la racine. La racine est au niveau 0.
4.2. Profondeur
La profondeur d’un nœud est un synonyme de son niveau.
4.3. Hauteur
La hauteur d’un arbre est le niveau maximal parmi tous les nœuds.
4.4. Taille
La taille d’un arbre est le nombre total de nœuds qu’il contient.
4.5. Degré d’un nœud
Le degré d’un nœud est le nombre d’enfants immédiats de ce nœud.
4.6. Sous-arbre
Un sous-arbre est constitué d’un nœud et de tous ses descendants.
On peut définir un arbre de manière récursive :
- un arbre est soit vide ;
- soit un nœud racine accompagné d’une liste de sous-arbres (ses enfants).
Chaque enfant d’un nœud est lui-même la racine d’un sous-arbre. C’est pour cela que les algorithmes sur les arbres (parcours, calcul de hauteur, comptage de nœuds, etc.) sont très souvent écrits à l’aide de fonctions récursives.
5. Parcours des arbres
Parcourir un arbre signifie visiter tous ses nœuds selon un certain ordre.
On distingue deux grandes familles :
- les parcours en profondeur (DFS) ;
- les parcours en largeur (BFS).
5.1. Parcours en profondeur (DFS)
Le parcours en profondeur (Depth First Search) consiste à explorer un chemin aussi loin que possible avant de revenir en arrière.
Dans un arbre général, on distingue notamment :
- Pré-ordre : on traite le nœud puis ses enfants ;
- Post-ordre : on traite d’abord les enfants, puis le nœud.
Idée générale en Python :
PROCÉDURE DFS(noeud)
traiter(noeud)
POUR CHAQUE enfant DANS noeud.enfants FAIRE
DFS(enfant)
FIN POUR
FIN PROCÉDURE
traiter(x) signifie : afficher, compter, accumuler…
5.2. Parcours en largeur (BFS)
Le parcours en largeur (Breadth First Search) visite l’arbre niveau par niveau, de la racine vers les feuilles.
Idée générale en Python :
PROCÉDURE BFS(racine)
file ← [racine]
TANT QUE file n’est pas vide FAIRE
n ← retirer_premier(file)
traiter(n)
POUR CHAQUE enfant DANS n.enfants FAIRE
ajouter_à_la_fin(file, enfant)
FIN POUR
FIN TANT QUE
FIN PROCÉDURE
6. Exemples réels d’arbres dans l’informatique
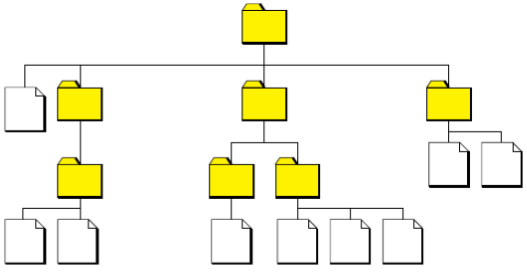
6.1. Système de fichiers
La structure d’un système de fichiers est naturellement un arbre : un dossier peut contenir des sous-dossiers, qui contiennent eux-mêmes d’autres dossiers ou des fichiers.
/
├── Documents
│ ├── Cours
│ └── NSI
├── Images
└── Musique
6.2. DOM HTML
L’organisation interne d’une page web (DOM) est un arbre enraciné :
la balise <html> est la racine,
qui contient <head> et <body>, etc.
6.3. Arbres syntaxiques
En compilation ou en analyse d’expressions mathématiques, on représente une expression
(par exemple (3 + 5) × 2) sous forme d’arbre : chaque opérateur est un nœud,
ses opérandes sont des enfants.
6.4. Arbres de décision
En intelligence artificielle, certains modèles (arbres de décision) prennent une décision en parcourant un arbre de questions/réponses, depuis une racine jusqu’à une feuille.